Seongho Jang
Ch.16 나이브 베이즈 분류 본문
1. 베이즈 추정
사후확률을 사전확률과 조건부확률의 결합으로 추정하는 방법



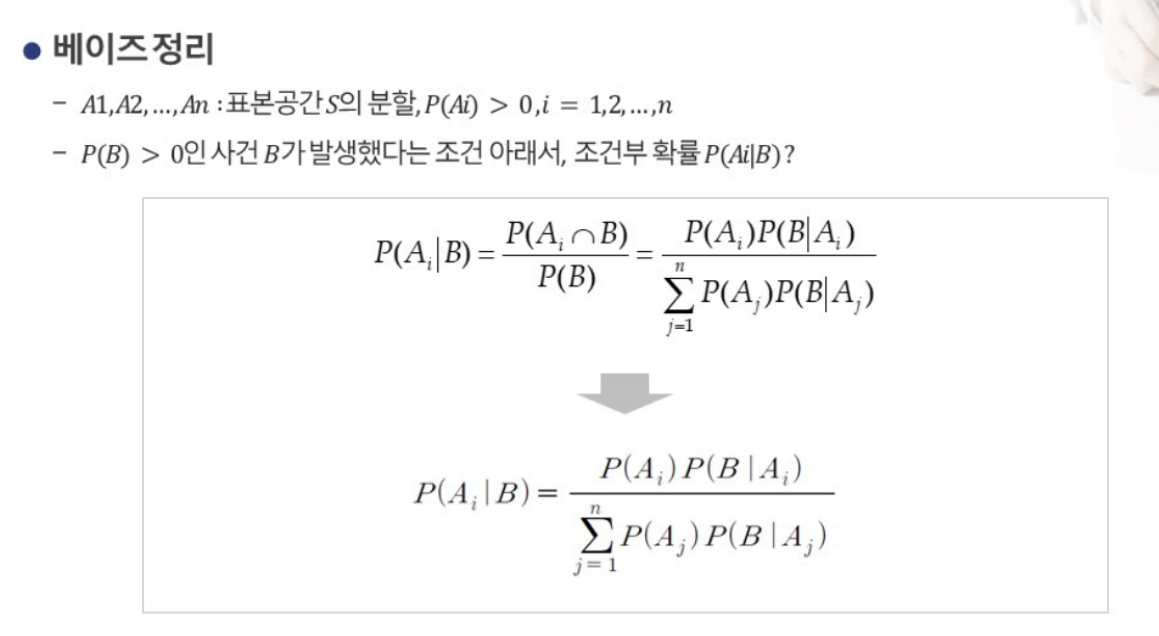

사건 B의 원인을 제공하는 확률 P(A)를 사전확률이라 하고,
사건 B가 일어난 이후의 확률P(A|B)을 사후확률이라 함
2. 나이브 베이즈
Feature들이 모두 동등하게 중요하며 독립적이라는 가정
결론적으로 나이브 베이즈는 분자 (P(A)P(A|B)) 기준으로 숫자가 큰 쪽으로 분류

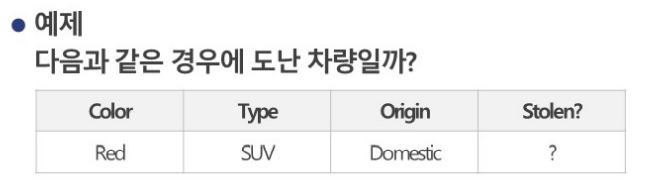
P(Yes|X) = P(Red|Yes) * P(SUV|Yes) * P(Domestic|Yes) * P(Yes) = 0.6 * 0.2 * 0.5 * 0.5 = 0.024
P(No |X) = P(Red|No) * P(SUV|No) * P(Domestic|No) * P(No) = 0.4 * 0.6 * 0.6 * 0.5 = 0.072
따라서 분류는 No.
만약 메일의 본문에 있는 단어가 3개라고 가정해보겠습니다. 기본적으로 나이브 베이즈 분류기는 모든 단어가 독립적이라고 가정합니다. 메일의 본문에 있는 단어 3개를 w1, w2, w3라고 표현한다면 결국 나이브 베이즈 분류기의 정상 메일일 확률과 스팸 메일일 확률을 구하는 식은 아래와 같습니다.
P(정상 메일 | 입력 텍스트) = P(w1 | 정상 메일) × P(w2 | 정상 메일) × P(w3 | 정상 메일) × P(정상 메일)
P(스팸 메일 | 입력 텍스트) = P(w1 | 스팸 메일) × P(w2 | 스팸 메일) × P(w3 | 스팸 메일) × P(스팸 메일)
식을 보고 눈치채신 분들도 있겠지만, 나이브 베이즈 분류기에서 토큰화 이전의 단어의 순서는 중요하지 않습니다. 즉, BoW와 같이 단어의 순서를 무시하고 오직 빈도수만을 고려합니다.
출처 : https://wikidocs.net/22892
3. Gaussian NB
from sklearn.naive_bayes import GaussianNBdf = pd.read_csv('iris.csv')
df["is_setosa"] = (df["Species"] == "setosa") + 0
df["is_setosa"].value_counts(normalize = True)is_setosa 분류하는 방법 잘 알아두기(True면 1, False면 0을 이용)


normalize 했을때와 안했을때의 결과 참고
문제 1
BMI가 0 초과인 데이터만을 사용하여 나이브 베이즈 분류를 실시하고자 한다. Outcome을 종속변수로 하고 나머지 변수를 독립변수로 할 때, 종속변수의 사전확률은?
df = pd.read_csv('diabetes.csv')
df_sub = df.loc[df["BMI"] > 0,]
df_sub["Outcome"].value_counts(normalize=True)BMI가 0 초과인것만 구분해내면 쉬운 문제인 것 같다. loc와 iloc 사용법을 더 정리해야 할것같다.
문제 2
혈당, 혈압, 나이를 독립변수로 하고 당뇨 발병 여부를 종속변수로 했을 때, 그 정확도는 얼마인가?
df = pd.read_csv('diabetes.csv')
model = GaussianNB().fit(X = df.loc[:, ["Glucose", "BloodPressure", "Age"]],
y = df["Outcome"])
pred = model.predict_proba(df.loc[:, ["Glucose", "BloodPressure", "Age"]])
pred_class = (pred[:, 1] > 0.5) + 0
accuracy_score(y_pred = pred_class, y_true = df["Outcome"])
predict_proba의 출력은 각 클래스에 대한 확률이고 decision_function의 출력보다 이해하기 더 쉽습니다. 이진 분류에서는 항상 사이즈가 (n_samples, 2)
각 행의 첫 번째 원소는 첫 번째 클래스의 예측 확률이고 두번째 원소는 두 번째 클래스의 예측 확률입니다. 확률이기 때문에 predict_proba의 출력은 항상 0과 1 사이의 값이며 두 클래스에 대한 확률의 합은 항상 1입니다.
print("확률 값의 형태: {}".format(gbrt.predict_proba(X_test).shape))
확률 값의 형태: (25, 2)
출처 : https://subinium.github.io/MLwithPython-2-4/
이 문제에서는 predict_proba의 두 번째 열이 문제에서 찾는 Outcome 값이다 (pred_class = (pred[:, 1] > 0.5) + 0).
이게 고정인지는 잘 모르겠다...
문제 3
임신여부, 연령대, BMI, 혈당을 독립변수로 하고 당뇨 발병 여부를 종속변수로 했을 때, 나이브 베이즈와 로지스틱 회귀 분석을 실시하고 둘 중 정확도가 높은 모델은?
df = pd.read_csv('diabetes.csv')
df2 = df.loc[df["BMI"] > 0, ]
df2["Age2"] = (df["Age"] // 10) * 10
df2["is_preg"] = (df["Pregnancies"] > 0) + 0
from sklearn.model_selection import train_test_split
df_train, df_test = train_test_split(df2, train_size = 0.8, test_size = 0.2, random_state = 123)
# 나이브 베이즈 정확도 계산
model = GaussianNB().fit(X = df_train.loc[:, ["is_preg", "BMI", "Glucose", "Age2"]], y = df_train["Outcome"])
pred = model.predict_proba(df_test.loc[:, ["is_preg", "BMI", "Glucose", "Age2"]])
accuracy_score(y_true = df_test["Outcome"],
y_pred = (pred[:, 1] > 0.5) + 0)
# Result = 0.8026315789473685
# 로지스틱 회귀 정확도 계산
from sklearn.linear_model import LogisticRegression
model_lr = LogisticRegression()
model_lr.fit(X = df_train.loc[:, ["is_preg", "BMI", "Glucose", "Age2"]],
y = df_train["Outcome"])
pred_lr = model_lr.predict_proba(df_test.loc[:, ["is_preg", "BMI", "Glucose", "Age2"]])
accuracy_score(y_true = df_test["Outcome"],
y_pred = (pred_lr[:, 1]> 0.5) + 0)
# Result = 0.8289473684210527험난했찌만 결국 해결했던 문제!
'Data Science Lv.2' 카테고리의 다른 글
| Ch.6 - 7 데이터 전처리(1): 결측치, 이상치, 파생변수 생성 (0) | 2023.01.06 |
|---|---|
| Ch.18 의사결정나무 (0) | 2023.01.03 |
| Ch.17 KNN (0) | 2023.01.02 |
| Ch.15 로지스틱 회귀분석 (0) | 2023.01.02 |
| Ch.13 비계층적 군집분석 (0) | 2023.01.01 |